Ch. 4 Pengukuran Gejala Pusat
Ukuran
gejala pusat merupakan suatu usaha yang ditujukan untuk mengukur
besarnya nilai rata-rata dari distribusi data yang telah diperoleh dalam
suatu penelitian. Untuk mengukur besarnya nilai rata-rata, maka yang
perlu dilakukan adalah membedakan secara jelas pengelompokkan data,
yaitu antara data tidak berkelompok dengan data berkelompok. Disamping
itu pengelompokkan data tersebut, juga perlu mempertimbangkan metode
yang digunakan dalam suatu penelitian, apakah berdasarkan data populasi
atau data sampel.
Rata-rata dengan ”Skala d” diperoleh : [(CI Σ di.Fri)/(ΣFr)]+Xi0 = [(10(1)) / 50)] + 114,5 = 114,7 kg
Ukuran yang dihitung dari
kumpulan data dalam sampel dinamakan statistik. Sedangkan ukuran yang
dihitung dari kumpulan data populasi atau dipakai untuk menyatakan
populasi dinamakan parameter. Jadi ukuran yang sama dapat bernama
statistik atau parameter bergantung pada apakah ukuran dimaksud untuk
sampel atau populasi.
Means/Rata-Rata Hitung Data Berkelompok
Untuk
mencari rata-rata hitung data berkelompok hampir sama dengan rata-rata
hitung data tidak berkelompok. Perbedaannya adalah jika dalam rata-rata
hitung data tidak berkelompok merupakan nilai penjumlahan X dibagi
dengan N, dimana nilai X adalah nilai absolut, sedangkan untuk rata-rata
hitung data berkelompok nilai X adalah nilai tengah masing-masing
kelas. Dengan demikian rata-rata hitung data berkelompok merupakan
penjumlahan nilai tenganh dengan frekuensi masing-masing kelas dibagi
dengan jumlah frekuensi atau dengan rumus: Rata-rata = (Σ Fr.Xi)/(ΣFr).
Keterangan : Fr adalah frekuensi ; Xi adalah nilai tengah.
Contoh :
Tabel : Persediaan Beras (dalam kg) dari 50 Pedagang di kota “X’ tanggal 31 Desember
Persediaan Beras
|
Jumlah Pedagang (Fr)
|
Nilai Tengah (X i)
|
( Fr x X i )
|
90 – 99
|
2
|
94,5
|
189,0
|
100 – 109
|
20
|
104,5
|
2.090,0
|
110 – 119
|
13
|
114,5
|
1.488,5
|
120 – 129
|
7
|
124,5
|
871,5
|
130 – 139
|
6
|
134,5
|
807,0
|
140 – 149
|
2
|
144,5
|
189,0
|
Jumlah
|
50
|
5.735,0
|
Rata-rata
hitung data pada tabel di atas adalah : (Σ Fr.Xi)/(ΣFr) = 5.735 / 50 =
114,7 kg. Jadi rata-rata hitung persedian beras dari 50 pedagang di kota
“X” per 31 Desember adalah sebesar 114,7 kg.
Dalam mencari
rata-rata hitung data berkelompok, disamping dengan menggunakan rumus
seperti tersebut di atas, dapat juga dengan menggunakan rumus “Skala d”,
yaitu: [(CI Σ di.Fri)/(ΣFr)]+Xi0. Keterangan : CI = class interval ; Xi
0 : class mark pada d = 0
Tabel : Persediaan Beras (dalam kg) dari 50 Pedagang di kota “X’ tanggal 31 Desember
Persediaan Beras
|
(Fr)
|
Nilai Tengah (X i)
|
Skala d
|
(d i x Fr i)
|
90 – 99
|
2
|
94,5
|
- 2
|
- 4
|
100 – 109
|
20
|
104,5
|
- 1
|
- 20
|
110 – 119
|
13
|
114,5
|
0
|
0
|
120 – 129
|
7
|
124,5
|
1
|
7
|
130 – 139
|
6
|
134,5
|
2
|
12
|
140 – 149
|
2
|
144,5
|
3
|
6
|
Jumlah
|
50
|
1
|
Median
Pengertian : Median merupakan nilai yang
berada di tengah atau rata-rata dari dua nilai yang berada di tengah
(jika data jumlah genap), setelah data tersebut diurutkan mulai dari
yang terkecil sampai dengan yang terbesar. Atau, median adalah nilai
tengah suatu kelompok data dimana data itu terbagi dua.
Untuk mencari nilai median pada data berkelompok dengan langkah sebagai berikut :
· Menentukan letak mendian dengan rumus n / 2
· Mencari nilai frekuensi komulatif kurang dari masing-masing kelas
· Nilai median dicari dengan rumus :
Md = CB b + CI (j / Fr m)
CB b = Class boundari bawah dari kelas yang mengandung median
CI = Class Interval
j = Selisih antara letak median dengan frekuensi komulatif pada kelas sebelum kelas yang mengandung median
Fr m = Frekuensi pada kelas yang mengandung median
Contoh :
Tabel : Persediaan Beras (dalam kg) dari 50 Pedagang di kota “X’ tanggal 31 Desember
Persediaan Beras
|
Jumlah Pedagang (Fr)
|
Fr Komulatif
|
90 – 99
|
2
|
2
|
100 – 109
|
20
|
22
|
110 – 119
|
13
|
35
|
120 – 129
|
7
|
42
|
130 – 139
|
6
|
48
|
140 – 149
|
2
|
50
|
Jumlah
|
50
|
Letak median adalah n / 2 = 50 / 2 = 25, yaitu terkandung pada kelas III (terkandung dalam frekuensi komulatif : 35).
Class boundary bawah kelas III = 109,5 ; Class Interval = 10 ; Nilai j = 25 – 22 = 3 ; Nilai Fr m = 13
Nilai median : Md = CB b + CI (j / Fr m) = 109,5 + 10 (3 / 13) = 111,81 kg.
Jadi persediaan beras dari 50 pedagang di kota “X” nilai tengah atau mediannya sebesar 111,81 kg.
Modus
Pengertian
: Modus (mode) dari sejumlah pengamatan adalah nilai X yang paling
banyak tampil. Oleh karena itu, dalam sekelompok data mungkin saja tidak
memiliki modus. Modus merupakan suatu pengamatan dalam distribusi
frekuensi yang memiliki jumlah pengamatan dimana jumlah frekuensinya
paling besar atau paling banyak. Untuk mencari nilai modus pada data
berkelompok dengan menggunakan langkah sebagai berikut :
Menentukan
letak modus, yaitu dilihat pada frekuensi terbesar atau jika frekuensi
terbesar lebih dari satu dapat dipilih salah satu. Jika mengamati gambar
polygon atau kurva letak modus adalah pada puncak gambar polygon atau
kurva. Menentukan nilai modus dengan rumus : Mo = CB b + CI [( D1 ) / (
D1 + D2 )]
Keterangan : D1 : Selisih frekuensi yang terdapat letak
modus dengan frekuensi sebelum letak modus. D2 : Selisih frekuensi yang
terdapat letak modus dengan frekuensi setelah letak modus.
Contoh : Tabel : Persediaan Beras (dalam kg) dari 50 Pedagang di kota “X’ tanggal 31 Desember
Persediaan Beras
|
Jumlah Pedagang (Fr)
|
90 – 99
|
2
|
100 – 109
|
20
|
110 – 119
|
13
|
120 – 129
|
7
|
130 – 139
|
6
|
140 – 149
|
2
|
Jumlah
|
50
|
Letak
modus berada di kelas II, yaitu frekuensi terbesar bernilai 20. Nilai
Modus adalah : Mo = 99,5 + 10 [(20 – 2) / ((20 – 2) + (20 – 13))] =
106,7. Jadi kebanyakan persediaan beras dari 50 pedagang (modusnya)
adalah sebanyak 106,7 kg.
Ch. 5 Kuartil, Nilai Rata Ukur, Nilai Rata Harmonik
KUARTIL
Jika sekumpulan data dibagi menjadi empat bagian
yang sama banyak, sesudah disusun menurut urutan nilainya, maka bilangan
pembaginya disebut dengan kuartil. Simbol kuartil adalah K. Dengan
demikian, ada tiga buah kuartil, yaitu K1, K2, dan K3. Pemberian nama
dimulai dari nilai kuartil yang paling kecil. Untuk menentukan nilai
kuartil, caranya adalah sebagai berikut.
1. Susun data menurut urutan nilainya, dari terkecil ke terbesar
2. Tentukan letak kuartil
3. Tentukan nilai kuartil
Letak kuartil ke-i, diberi lambang Ki, ditentukan dengan rumus sbb.
Contoh
Sampel data
27 30 28 29 22 25 24 23 24 25 27 31 21 26
Setelah disusun,
21 22 23 24 24 25 25 26 27 27 28 29 30 31
yaitu antara data ke-3 dengan data ke-4 dan 0,75 unit jauhnya dari data ke-3
Dengan demikian,
nilai K1 = data ke-3 + 0,75(data ke-4 - data ke-3)
K1 = 23 + 0,75(24-23) = 23,75
yaitu antara data ke-7 dengan data ke-8 dan 0,5 unit jauhnya dari data ke-7
Dengan demikian,
nilai K2 = data ke-7 + 0,5(data ke-8 - data ke-7)
K2 = 25 + 0,5(26-25) = 25,5
yaitu antara data ke-11 dengan data ke-12 dan 0,25 unit jauhnya dari data ke-11
Dengan demikian,
nilai K3 = data ke-11 + 0,25(data ke-12 - data ke-11)
K3 = 28 + 0,25(29-28) = 28,25
Rata-rata Ukur (Geometric Mean)
a. Pengertian Nilai Rata-rata UkurNilai rata-rata ukur dari sekelompok bilangan ialah hasil perkalian bilangan tersebut, diakar pangkatkan sebanyaknya bilangan itu sendiri.
Rata rata ukur dipakai untuk menggambarkan keseluruhan data khususnya bila data tersebut mempunyai ciri tertentu yaitu banyaknya nilai data yang satu sama lain saling berkelipatan sehingga perbandingan tiap dua data yang berurutan tetap atau hampir tetap. Bila suatu kelompok data mempunyai ciri seperti ini maka rata rata ukur akan lebih baik dari pada rata rata hitung.
b. Cara menghitung nilai rata-rata ukur
Untuk Data Tidak Berkelompok
n
G = √ ( X1, X2, X3….Xn
) Untuk Data yang Kecil
( ∑ log X )
G = antilog (
------------------- ) Untuk Data yang Besar
∑ n
·
Untuk Data Berkelompok
( ∑ f . log X )
G = antilog (
------------------- )
∑ f
Contoh: Tentukan rata rata ukur (GEOMETRIC MEAN) data 2, 4,
8
Jawab :
n = 3
Log 2 = 0,3010
Log 4 = 0,6021
Log 8 = 0,9031
Maka Log 2 + Log
4 + Log 8 = 0,3010 + 0,6021 + 0,9031 = 1,8062
(
∑ log X )
G = antilog (
------------------- )
∑ n
( Log 2 + Log 4 + Log 8 )
G = antilog (
------------------------------------- )
3
( 1,8062 )
G = antilog (
------------------ ) = antilog 0,6021 = 4
Rata-rata Harmonik
Rata-rata harmonik dari suatu kumpulan data x1, x2, …, xn adalah kebalikan dari nilai rata-rata hitung (aritmetik mean). Secara matematis dapat dinyatakan dengan formula berikut:

Secara umum, rata-rata harmonic jarang digunakan. Rata-rata ini hanya digunakan untuk data yang bersifat khusus. Misalnya,rata-rata harmonik sering digunakan sebagai ukuran tendensi sentral untuk kumpulan data yang menunjukkan adanya laju perubahan, seperti kecepatan.
Contoh 1:Si A bepergian pulang pergi. Waktu pergi ia mengendarai kendaraan dengan kecepatan 10 km/jam, sedangkan waktu kembalinya 20 km/jam. Berapakah rata-rata kecepatan pulang pergi?
Jawab:Apabila kita menghitungnya dengan menggunakan rumus jarak dan kecepatan, tentu hasilnya 13.5 km/jam!
Apabila kita gunakan perhitungan rata-rata hitung, hasilnya tidak tepat!
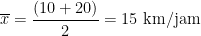
Pada kasus ini, lebih tepat menggunakan rata-rata harmonik:
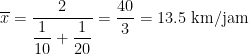
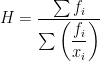
Contoh 2:
Berapa rata-rata Harmonik dari tabel distribusi frekuensi pada Contoh 3 pada Tendensi Sentral: Mean!
Jawab:
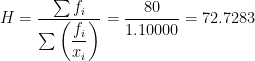
Secara umum, rata-rata harmonic jarang digunakan. Rata-rata ini hanya digunakan untuk data yang bersifat khusus. Misalnya,rata-rata harmonik sering digunakan sebagai ukuran tendensi sentral untuk kumpulan data yang menunjukkan adanya laju perubahan, seperti kecepatan.
a. Rata-rata harmonic untuk data tunggal
Contoh 1:Si A bepergian pulang pergi. Waktu pergi ia mengendarai kendaraan dengan kecepatan 10 km/jam, sedangkan waktu kembalinya 20 km/jam. Berapakah rata-rata kecepatan pulang pergi?
Jawab:Apabila kita menghitungnya dengan menggunakan rumus jarak dan kecepatan, tentu hasilnya 13.5 km/jam!
Apabila kita gunakan perhitungan rata-rata hitung, hasilnya tidak tepat!
Pada kasus ini, lebih tepat menggunakan rata-rata harmonik:
b. Rata-rata Harmonik untuk Distribusi Frekuensi:
Contoh 2:
Berapa rata-rata Harmonik dari tabel distribusi frekuensi pada Contoh 3 pada Tendensi Sentral: Mean!
Jawab:
| Kelas ke- | Nilai Ujian | fi | xi | fi/xi |
| 1 | 31 – 40 | 2 | 35.5 | 0.0563 |
| 2 | 41 – 50 | 3 | 45.5 | 0.0659 |
| 3 | 51 – 60 | 5 | 55.5 | 0.0901 |
| 4 | 61 – 70 | 13 | 65.5 | 0.1985 |
| 5 | 71 – 80 | 24 | 75.5 | 0.3179 |
| 6 | 81 – 90 | 21 | 85.5 | 0.2456 |
| 7 | 91 – 100 | 12 | 95.5 | 0.1257 |
| 8 | Jumlah | 80 | 1.1000 |
Ch. 6 Pengukuran Penyimpanan (Range - Deviasi - Varian)
Varian
Varians adalah salah satu ukuran dispersi atau
ukuran variasi. Varians dapat menggambarkan bagaimana berpencarnya
suatu data kuantitatif. Varians diberi simbol σ2 (baca: sigma kuadrat) untuk populasi dan untuk s2 sampel.
Selanjutnya kita akan menggunakan simbol s2 untuk varians karena umumnya kita hampir selalu berkutat dengan sampel dan jarang sekali berkecimpung dengan populasi.
Rumus untuk menghitung varians ada dua , yaitu rumus
teoritis dan rumus kerja. Namun demikian, untuk mempersingkat tulisan
ini, maka kita gunakan rumus kerja saja. Rumus kerja ini mempunyai
kelebihan dibandingkan rumus teoritis, yaitu hasilnya lebih akurat dan
lebih mudah mengerjakannya.
Rumus kerja untuk varians adalah sebagai berikut
Contoh
Data jumlah anakan padi varietas Pandan Wangi pada metode SRI adalah sebagai berikut
28 32 15 21 30 30 27 22 36 40
Sampel
|
y
|
y2
|
1
|
28
|
784
|
2
|
32
|
1024
|
3
|
15
|
225
|
4
|
21
|
441
|
5
|
30
|
900
|
6
|
30
|
900
|
7
|
27
|
729
|
8
|
22
|
484
|
9
|
36
|
1296
|
10
|
40
|
1600
|
Jumlah
|
281
|
8383
|
Maka nilai varians data di atas adalah
Deviasi
Standar deviasi disebut juga simpangan baku.
Seperti halnya varians, standar deviasi juga merupakan suatu ukuran
dispersi atau variasi. Standar deviasi merupakan ukuran dispersi yang
paling banyak dipakai. Hal ini mungkin karena standar deviasi mempunyai
satuan ukuran yang sama dengan satuan ukuran data asalnya. Misalnya,
bila satuan data asalnya adalah cm, maka satuan standar deviasinya juga
cm. Sebaliknya, varians memiliki satuan kuadrat dari data asalnya
(misalnya cm2). Simbol standar deviasi untuk populasi adalah σ (baca: sigma) dan untuk sampel adalah s.
Rumus untuk menghitung standar deviasi adalah sebagai berikut
Contoh:
Data umur berbunga (hari) tanaman padi varietas Pandan Wangi adalah sbb: 84 86 89 92 82 86 89 92 80 86 87 90
Berapakah standar deviasi dari data di atas?
Sampel
|
y
|
y2
|
1
|
84
|
7056
|
2
|
86
|
7396
|
3
|
89
|
7921
|
4
|
92
|
8464
|
5
|
82
|
6724
|
6
|
86
|
7396
|
7
|
89
|
7921
|
8
|
92
|
8464
|
9
|
80
|
6400
|
10
|
86
|
7396
|
11
|
87
|
7569
|
12
|
90
|
8100
|
Jumlah
|
1043
|
90807
|
Maka nilai standar deviasi data di atas adalah

STANDAR DEVIASI
Standar deviasi disebut juga simpangan baku.
Seperti halnya varians, standar deviasi juga merupakan suatu ukuran
dispersi atau variasi. Standar deviasi merupakan ukuran dispersi yang
paling banyak dipakai. Hal ini mungkin karena standar deviasi mempunyai
satuan ukuran yang sama dengan satuan ukuran data asalnya. Misalnya,
bila satuan data asalnya adalah cm, maka satuan standar deviasinya juga
cm. Sebaliknya, varians memiliki satuan kuadrat dari data asalnya
(misalnya cm2). Simbol standar deviasi untuk populasi adalah σ (baca: sigma) dan untuk sampel adalah s.
Rumus untuk menghitung standar deviasi adalah sebagai berikut
Contoh:
Data umur berbunga (hari) tanaman padi varietas Pandan Wangi adalah sbb: 84 86 89 92 82 86 89 92 80 86 87 90
Berapakah standar deviasi dari data di atas?
Sampel
|
y
|
y2
|
1
|
84
|
7056
|
2
|
86
|
7396
|
3
|
89
|
7921
|
4
|
92
|
8464
|
5
|
82
|
6724
|
6
|
86
|
7396
|
7
|
89
|
7921
|
8
|
92
|
8464
|
9
|
80
|
6400
|
10
|
86
|
7396
|
11
|
87
|
7569
|
12
|
90
|
8100
|
Jumlah
|
1043
|
90807
|
Maka nilai standar deviasi data di atas adalah

STANDAR DEVIASI
Standar deviasi disebut juga simpangan baku.
Seperti halnya varians, standar deviasi juga merupakan suatu ukuran
dispersi atau variasi. Standar deviasi merupakan ukuran dispersi yang
paling banyak dipakai. Hal ini mungkin karena standar deviasi mempunyai
satuan ukuran yang sama dengan satuan ukuran data asalnya. Misalnya,
bila satuan data asalnya adalah cm, maka satuan standar deviasinya juga
cm. Sebaliknya, varians memiliki satuan kuadrat dari data asalnya
(misalnya cm2). Simbol standar deviasi untuk populasi adalah σ (baca: sigma) dan untuk sampel adalah s.
Rumus untuk menghitung standar deviasi adalah sebagai berikut
Contoh:
Data umur berbunga (hari) tanaman padi varietas Pandan Wangi adalah sbb: 84 86 89 92 82 86 89 92 80 86 87 90
Berapakah standar deviasi dari data di atas?
Sampel
|
y
|
y2
|
1
|
84
|
7056
|
2
|
86
|
7396
|
3
|
89
|
7921
|
4
|
92
|
8464
|
5
|
82
|
6724
|
6
|
86
|
7396
|
7
|
89
|
7921
|
8
|
92
|
8464
|
9
|
80
|
6400
|
10
|
86
|
7396
|
11
|
87
|
7569
|
12
|
90
|
8100
|
Jumlah
|
1043
|
90807
|
Maka nilai standar deviasi data di atas adalah

Range
Range adalah selisih antara nilai terbesar ( nilai maksimum ) dengan
nilai terkecil ( nilai minimum ) pada suatu gugus data. Range bukan
merupakan ukuran penyebaran data yang baik karena ukuran ini hanya
memperhatikan kedua nilai ekstrem dan tidak mengatakan apa-apa mengenai
sebaran bilangan-bilangan yang ada diantara kedua nilai ekstrem
tersebut.
Range = Nilai Maksimum – Nilai Minimum
Range = Nilai Maksimum – Nilai Minimum
DAFTAR PUSTAKA
Agus Irianto. (2010). Statistika Konsep, Dasar, Aplikasi, dan Pengembangannya. Jakarta: Kencana Prenada Media Group.
Ronald E. Walpole. (1995). Pengantar Statistika Edisi ke-3. Jakarta: Gramedia Pustaka Utama
Sugiyono. (2010). Statistika untuk Penelitian. Bandung: Alfabeta
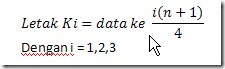
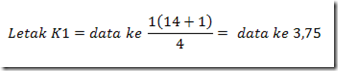
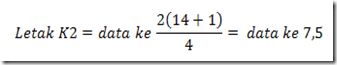
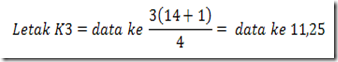
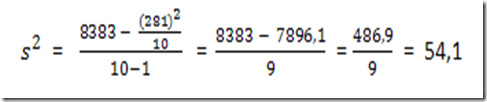
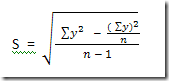
Makasih gan materi statistiknya
BalasHapusoya, kunjungi blog saya ya di
Ikubaru Blogzia: Statistik